내적과 코사인 유사도가 어떤 연관이 있는지 정리해 보겠습니다.
내적 (Dot product / Scalar product)
- 여러 가지 연산 중 하나의 연산이다.
- 벡터와 벡터의 연산
- 결괏값은 스칼라
- 공식 : a • b = |a| * |b| * cos θ
코사인 유사도 (Cosine Similarity)
- 두 벡터 사이의 각도를 계산해 두 벡터의 유사도를 측정하는 척도
- 1에 가까울수록 두 벡터가 유사하다고 해석
- 유사도는 두 벡터가 가리키는 방향의 유사도를 의미
- 방향이 같다면 코사인 유사도는 1, 직교한다면 0, 정반대의 방향이라면 -1로 표현한다.
코사인 유사도에서 내적
내적의 공식을 다시 살펴보면, a • b = |a| * |b| * cos θ이다.
두 벡터의 크기와 두 벡터가 이루는 각의 코사인 값을 곱한다.
여기에서 코사인의 성질을 이용할 수 있다.
코사인은 두 벡터가 직교하면 0, 90도보다 큰 각이면 음수값을 가진다.
이 점을 이용하면 두 벡터의 내적만으로도 두 벡터의 방향을 알 수 있다.
이 성질을 이용해서 우리는 두 벡터의 유사도를 각도를 직접 계산하는 것이 아닌 코사인 값으로 측정한다.
왜 코사인 유사도 ?
유사도를 측정할 수 있는 다른 방법도 존재한다.
두 벡터의 거리를 측정하는 유클리드 거리 계산법이 있다.
하지만 유클리드 거리 계산은 두 벡터의 성향이 아닌 값에 영향을 많이 받게 된다.
수식을 보면 벡터의 값 크기가 고려되는 것을 알 수 있다.
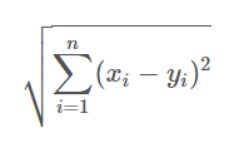
예시로 뉴질랜드의 지역 이름들의 유사도를 구해보자!
"오타와"와 "타우마 타와카탕이항아코아우아우오타마테아투리푸카카피키마웅아호로누쿠포카이웨누아키타나타후"의 유사도를 구하고자 한다.
놀랍게도 두 단어 모두 뉴질랜드의 지명 이름이다.
두 단어가 지명 이름이라는 것을 아는 순간, 인간은 직관적으로 두 단어의 공통점을 찾을 수 있다.
컴퓨터로는 어렵기 때문에, 거리를 계산해서 유사도를 구하려고 유클리드 거리를 계산하면, 이 두 단어의 유사성은 아주 희박하게 계산될 것이다. 코사인 유사도는 벡터의 양에 구애받지 않고, 성향(방향) 측면에서 유사성을 확인할 수 있기에 자연어처리에서 사용된다.
'ML & DL > NLP' 카테고리의 다른 글
| Word Embedding Association Test (WEAT) - 편향성 측정 (0) | 2021.11.08 |
|---|---|
| 텍스트 벡터화 기법의 종류 (2) | 2021.07.02 |
| 자연어 처리와 토크나이저 (0) | 2021.07.02 |
